Equation Derivation for Servo Motor

In the analysis of electric servo drive motors, the equations for the motor indicates the presence of two time constants. One is a mechanical time constant and the other is an electrical time constant. Commercial servo motor specifications usually list these two time constants. However, it should be cautioned that these two time constants as given in the specifications are for the motor alone with no load inertia connected to the motor shaft. Since these two time constants are part of the motor block diagram used in servo analysis, it is important to know the real value of the time constants under actual load conditions.
There are two types of servo motors to consider. The first is the classical dc servo motor and the second is the ac servo motor often referred to as a brushless dc motor.
A derivation of the motor equations and the electrical and mechanical motor time constants will be discussed for the dc motor followed by the ac motor. The dc motor equivalent diagram is:

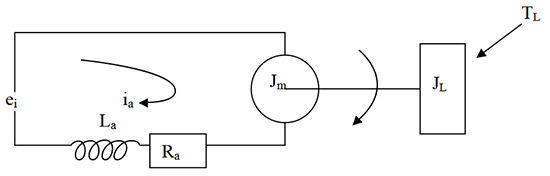
Where:

e_i= Applied voltage (volts)
i_a= Armature current (amps)
J_t= Total inertia of motor armature plus load (lb-in-sec²)
K_e= Motor voltage constant (v/rad/sec)
K_t= Motor torque constant (lb-in/A)
L_a= Motor winding inductance (Henries)
R_a= Armature resistance (ohms)
T_L= Load torque (lb-in)
V_m= Motor velocity (rad/sec)
α= Acceleration (rad/sec²)

The steady state (dc) equations are:

e_i= i_aR_a+K_eV_m          (Voltage equation)
t= Torque= i_aK_t=Jα  (Torque equation)

For the general case, the differential equations are:

e_i= i_aR_a+L_a(di_a/d_t)+K_eV_m
Laplace operator S=d/dt

e_i=R_ai_a + L_aSi_a + K_eV_m
e_i=(R_a + L_aS)i_a + K_eV_m
e_i=[(L_a/R_a)S+1]R_ai_a+ K_eV_m

Also:

T=K_ti_a=J_tα=J_tV_mS
i_a=T/K_t= J_tV_mS/K_t

Combining equations gives:

e_i-K_eV_m=[(L_a/R_a)S+1]R_a[(J_tV_mS)/K_t]

Rearranging results in:

[(e_i-K_eV_m)K_t]/{[(L_a/R_a)S+1]R_aJ_tS}=V_m

This last equation can be represented in block diagram form as:

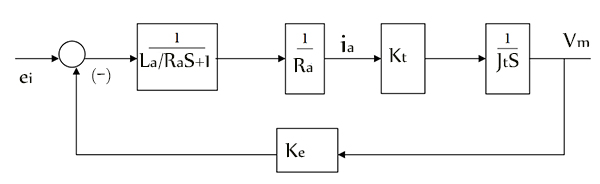
The closed loop equation C/R=G/(1+GH) for the above block diagram is:

V_m/e_i=K_t/{R_aJ_tS[(L_a/R_a)S+1]+K_eK_t}

Rearranging gives:

V_m/e_i=K_t/[R_aJ_t(L_a/R_a)S²+J_tR_aS+K_eK_t]

Dividing by K_eK_t gives:

V_m/e_i=(1/K_e)/[(R_aJ_t/K_eK_t)( L_a/R_a)S²+( R_aJ_t/K_eK_t)S+1]

From the last equation, the motor mechanical time constant, T_m, is:

T_m= R_aJ_t/K_eK_t    [sec]

The total inertia, J_r, is the sum of the reflected inertia to the motor shaft plus the motor inertia. The resistance, R_a, is the motor winding resistance plus the external circuit resistance. Thus the motor mechanical time constant is summarized as:

T_m=ΣR_aJ_t/K_eK_t

Also, the servo motor electrical time constant is:

T_e=L_a/ΣR_a  [sec]

Therefore, the closed loop motor equation can be expressed as:

V_m/e_i=(1/K_e)/(T_mT_eS²+T_mS+1)

From the general equation for a quadratic:

(S²/ω_m²)+(2δS/ω_m)+1

Where:

ω_m=(1/T_mT_e)^-2

The damping factor is:

δ=0.5 T_mω_m =0.5T_m(1/T_mT_e)^-2=0.5(T_m/T_e)^-2

The mechanical and electrical time constants for a brushless dc motor have the same basic equations with some variations. For a brushless dc motor with a wye connected motor, the electrical circuit is:

The mechanical time constant is:

T_m=ΣR_phaseJ_total/K_e(phase)K_t    [sec]

Where:

K_e(phase)=Motor voltage constant=K_e(L-L)/1.73 [(V-sec)/RAD]
K_t= Motor torque constant [(Ib-in)/A]
R_m(L-L)=Motor resistance [ohms]
ΣR_m(L-L)=Total motor circuit resistance=1.35 R_m(L-L)    [ohms]
ΣR_m(phase)=ΣR_m(L-L)×0.5=[ohms]
L_L-L=Motor inductance= [Henries]
J_TOTAL=Motor armature inertia plus the reflected load inertia at the motor shaft= [Ib-in-sec²]

Most manufacturers give the electrical parameters in line-to-line values. Thus some of these values must be converted to the phase values as shown above. Summarizing, the mechanical time constant can be computed as:

T_m=[Σ(R_L-L/2)J_TOTAL]/K_tK_e(L-L)/1.73 [sec] = 0.86(R_L-LJ_{total motor})/K_e(L-L)K_t

The electrical time constant for the brushless dc motor is computed as:

T_e=Total inductive path/ Total resistive path= L_L-L/ΣR_m(L-L) [sec]

Another factor affecting the mechanical time constant is the temperature. Most manufacturers specify the servo parameters at 25° C (cold rating). This implies that the magnet and wires are both at room temperature. However, the motors used in industry will operate hotter which could reach a magnet temperature of 80° C to 90°C in a 40° C ambient. The winding temperature is considerably more than that. Some means must be used to compensate for the motor parameters rated at 25° C. For those manufacturers that offer the hot rating on motor specification parameters, they should be used to calculate the time constants. The parameters of motor resistance, torque constant, and voltage constant should be adjusted, if needed, for the hot rating. The motor resistance will increase; the torque constant and voltage constant will decrease. However, contrary to their implied name both time constants are not of constant value. Rather, they are both functions of the motor’s operating temperature.